Math Notes

Predict the long-term behavior of polynomial functions without graphing:

• Analyze leading coefficient and degree
• Determine behavior as x approaches ±∞
• Understand even vs. odd degree patterns
• Interactive behavior predictor tool

Core concepts for polynomial graphs and equations:

• Finding intersection points
• Solving factorable equations
• Finding x-intercepts
• Graph behavior & degree

Fast method for dividing polynomials by linear factors:

• Quick polynomial division by $x - c$
• Step-by-step coefficient operations
• Find polynomial zeros and factors
• Worked examples with practice problems

Comprehensive reference for all polynomial concepts:

• Synthetic division and factoring methods
• Finding roots and constant terms
• Solving equations in factored form
• End behavior and graphing techniques

In the unit circle, we can visualize the relationship between sine and cosine functions. For any angle θ:

• sin(θ) represents the y-coordinate
• cos(θ) represents the x-coordinate
• The fundamental identity sin²(θ) + cos²(θ) = 1

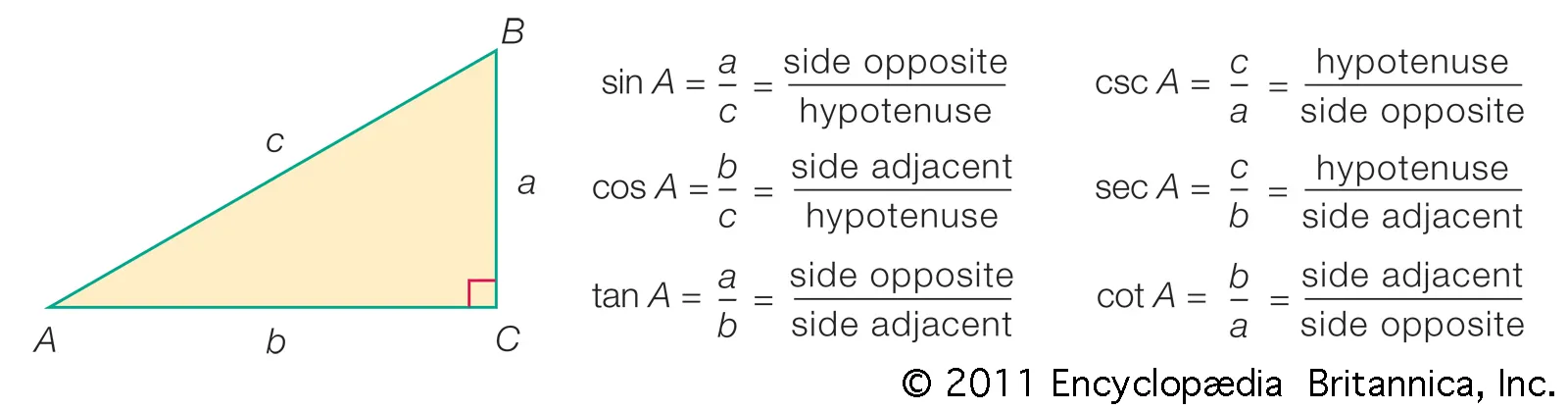
SOH CAH TOA is a mnemonic device to remember the trigonometric ratios for right triangles:

• SOH: Sine = Opposite / Hypotenuse
• CAH: Cosine = Adjacent / Hypotenuse
• TOA: Tangent = Opposite / Adjacent

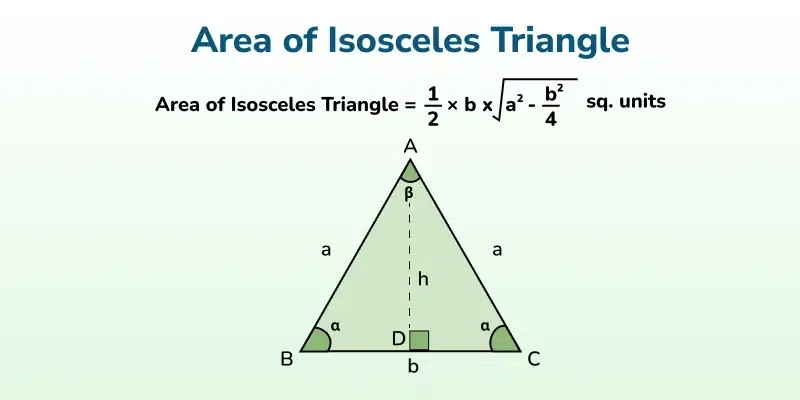
Learn different methods to calculate the area of triangles, including:

• Standard formula: A = ½ × base × height
• Area of right-angled triangles
• Area of equilateral triangles
• Heron's formula for any triangle

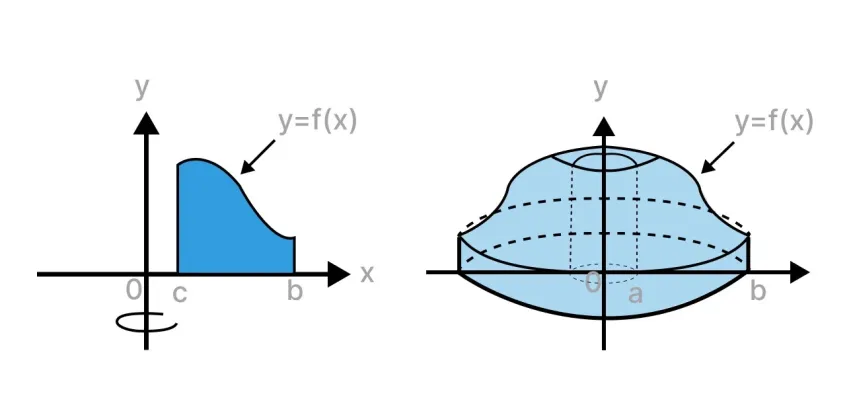
Learn how two-dimensional shapes can be rotated around an axis to create three-dimensional objects:

• Understand the concept of solids of rotation
• Explore common shapes like cylinders, cones
• Learn volume formulas for various solids
• See how calculus is applied

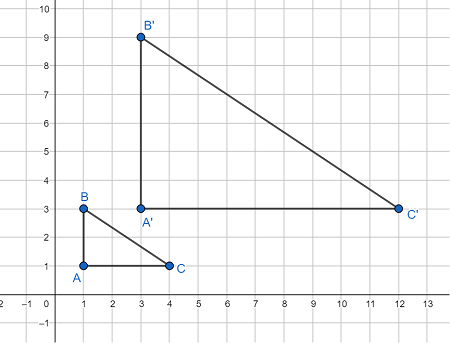
Master geometric transformations that change size while preserving shape:

• Understand scale factors and centers of dilation
• Calculate area changes with k² scaling
• Determine scale factors from given areas
• Apply dilations to solve real-world problems

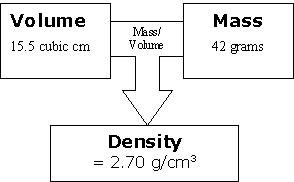
Explore the fundamental relationship between mass, volume, and density:

• Master the density formula: Density = Mass/Volume
• Convert between different units (g/cm³, kg/m³)
• Calculate any variable when given the other two
• Apply density concepts to real-world problems

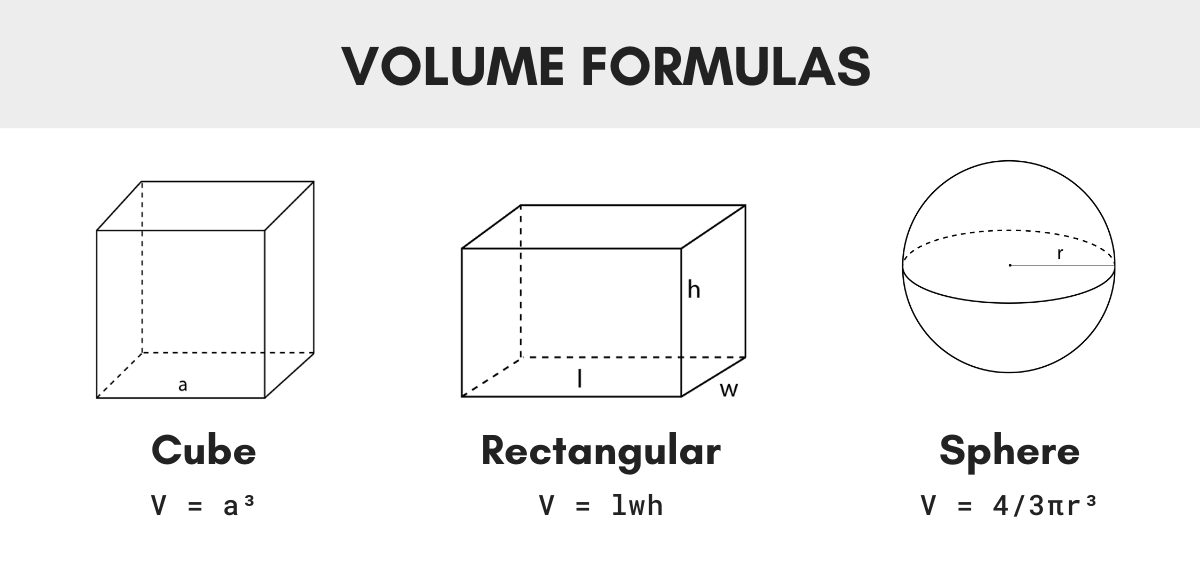
Calculate volumes of various three-dimensional geometric solids:

• Cylinders: V = πr²h or V = B×h
• Cones: V = (1/3)πr²h
• Pyramids: V = (1/3)×BaseArea×h
• Prisms: V = BaseArea×h